Cones | Geometrizandoo

Cones

Definição

Considere uma região plana limitada por uma curva suave (sem quinas), fechada e um ponto P fora desse plano. Chamamos de cone ao sólido formado pela reunião de todos os segmentos de reta que têm uma extremidade em P e a outra num ponto qualquer da região.

Introdução

Vídeo Aulas

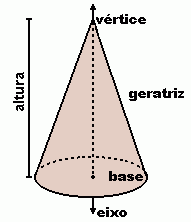
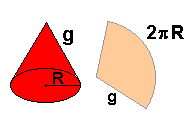
Base: A base do cone é a região plana contida no interior da curva, inclusive a própria curva.

Vértice: O vértice do cone é o ponto P.

Eixo: Quando a base do cone é uma região que possui centro, o eixo é o segmento de reta que passa pelo vértice P e pelo centro da base.

Geratriz: Qualquer segmento que tenha uma extremidade no vértice do cone e a outra na curva que envolve a base.

Altura: Distância do vértice do cone ao plano da base.

Superfície lateral: A superfície lateral do cone é a reunião de todos os segmentos de reta que tem uma extremidade em P e a outra na curva que envolve a base.

Superfície do cone: A superfície do cone é a reunião da superfície lateral com a base do cone que é o círculo.

Seção meridiana: A seção meridiana de um cone é uma região triangular obtida pela interseção do cone com um plano que contem o eixo do mesmo.

Elementos do COne

Classificação do COne

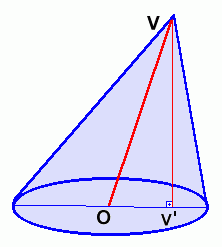
Quando observamos a posição relativa do eixo em relação à base, os cones podem ser classificados como retos ou oblíquos. Um cone é dito reto quando o eixo é perpendicular ao plano da base e é oblíquo quando não é um cone reto. Ao lado apresentamos um cone oblíquo.

Observação: Para efeito de aplicações, os cones mais importantes são os cones retos. Em função das bases, os cones recebem nomes especiais. Por exemplo, um cone é dito circular se a base é um círculo e é dito elíptico se a base é uma região elíptica.

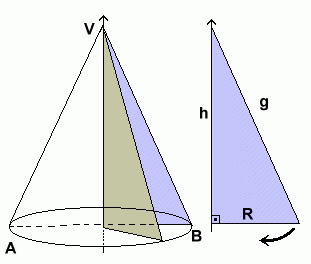
1.Um cone circular reto é chamado cone de revolução por ser obtido pela rotação (revolução) de um triângulo retângulo em torno de um de seus catetos

2. A seção meridiana do cone circular reto é a interseção do cone com um plano que contem o eixo do cone. No caso acima, a seção meridiana é a região triangular limitada pelo triângulo isósceles VAB.

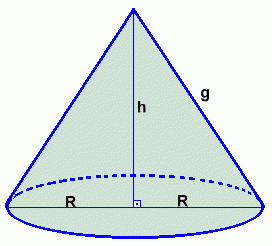
3. Em um cone circular reto, todas as geratrizes são congruentes entre si. Se g é a medida de cada geratriz então, pelo Teorema de Pitágoras, temos:

g2 = h2 + R2

Observações sobre um cone circular reto

4. A Área Lateral de um cone circular reto pode ser obtida em função de g (medida da geratriz) e R (raio da base do cone):

ALat = Pi R g

5. A Área total de um cone circular reto pode ser obtida em função de g (medida da geratriz) e R (raio da base do cone):

ATotal = Pi R g + Pi R2

Cones Equiláteros

Um cone circular reto é um cone equilátero se a sua seção meridiana é uma região triangular equilátera e neste caso a medida da geratriz é igual à medida do diâmetro da base.

A área da base do cone é dada por:

ABase=Pi R2

Pelo Teorema de Pitágoras temos:

(2R)2 = h2 + R2
h2 = 4R2 - R2 = 3R2

Assim:

h = R

Como o volume do cone é obtido por 1/3 do produto da área da base pela altura, então:

V = (1/3) Pi R³

Como a área lateral pode ser obtida por:

ALat = Pi R g = Pi R 2R = 2 Pi R2

então a área total será dada por:

ATotal = 3 Pi R²